コンデンサの故障と寿命(3)
~寿命推定~
はじめに
コンデンサは、回路の基本的かつ重要な電子部品のひとつです。代表的なコンデンサにはアルミ電解コンデンサ(Al-Ecap)、蒸着電極形フィルムコンデンサ(MF-cap)、積層セラミックコンデンサ(MLCC)、タンタルコンデンサ(Ta-Ecap)があり、回路の機能、サイズ、コストなどによって使い分けられています。一方で、製造時や使用時における過度なストレスや設計上のミスによって機能を失う故障や、発煙発火などのトラブルが起こることがあります。
本稿では、パワーエレクトロニクスで使われるAl-Ecap、MF-cap、MLCCを中心に故障モードと故障メカニズムを解説し、寿命推定と安全な使い方を解説します。
目次
寿命推定
寿命推定の基本
故障率とバスタブカーブ
コンデンサの基本的な性質でご説明したようにコンデンサの機能は
① 直流電流を通さない
② 瞬時に電荷を溜めたり放出したりする
③ 交流電流を通す
ことであり、これらの機能が失われたときに故障となります。
故障率(Failure Rate)は、「システムや部品等が、ある期間故障なく動作した後、引き続く単位期間内に故障を起こす割合」と定義されます*01。つまり故障率は「故障の起きる割合」であり、信頼性の定量的な尺度です。
*01 JIS C 5003-1974 電子部品の故障率試験方法通則
故障率は、図1に示す故障率曲線(バスタブカーブ)で時間依存性が表現され、(1) 稼動を開始してから比較的早い時期に発生する初期故障、(2)その後長い使用期間にわたって散発的に発生する偶発故障、(3) 本質的な寿命にともなって時間とともに増加する摩耗故障(耐用寿命)の三つの領域に分けられます。
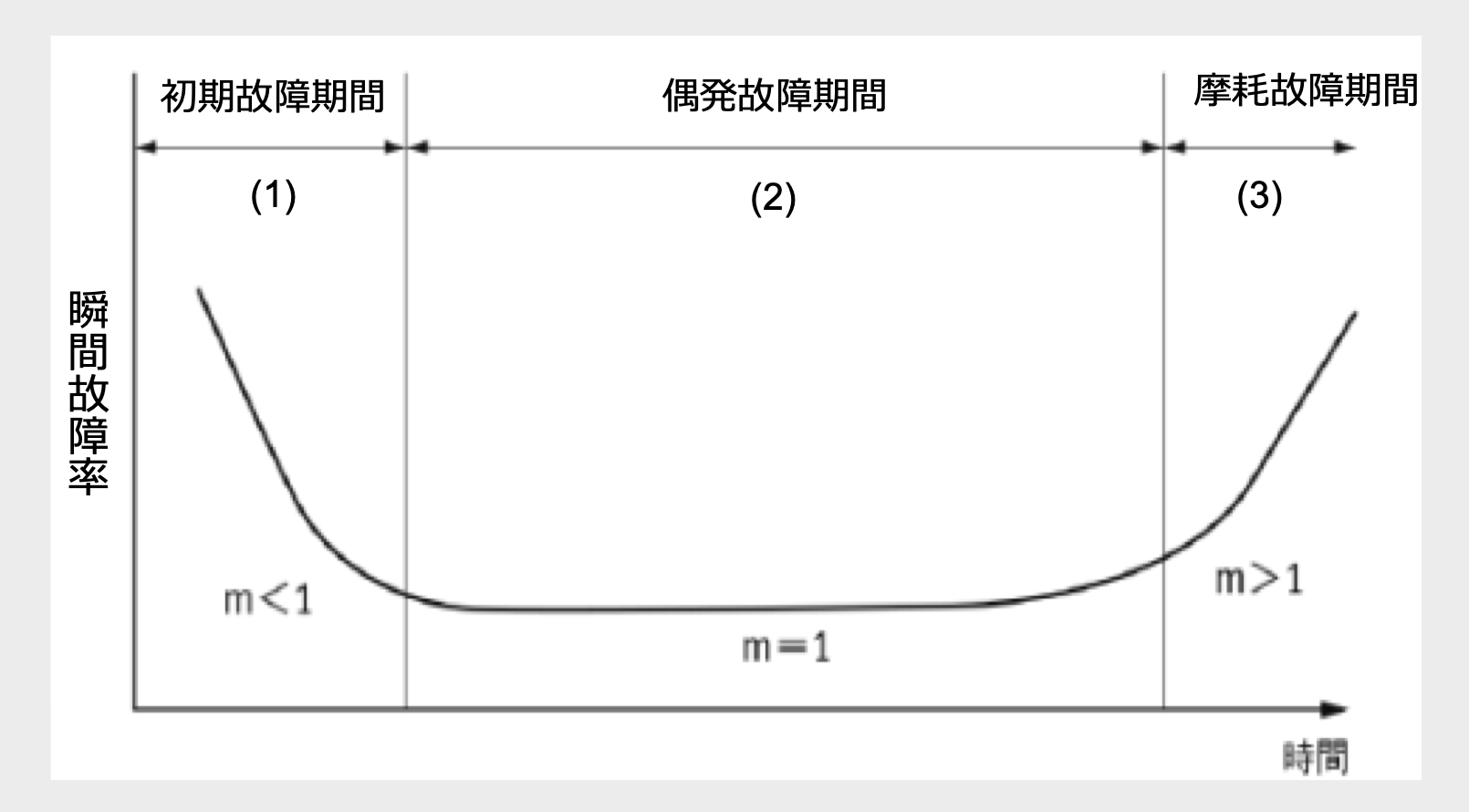
瞬間故障率の時間依存性(バスタブカーブ)
m : 形状パラメータ
初期故障と摩耗故障
初期故障
図1の(1)の領域は初期故障期間と呼ばれ、この期間の故障を初期故障と呼びます。初期故障は、FMEAでは捕らえられなかった潜在的な設計ミス、⼯程での⽋陥などさまざまな弱点が温度や電圧などのストレスによって短時間で顕在化することで発生します。
初期故障の発生率は時間の経過とともに減少するため、製造工程内で発見されて取り除かれることが可能な故障です。初期故障を取り除くプロセスをデバッギング(Debugging)といい、エージングやスクリーニングなどが⾏われます。当社では独自の品質管理手法と品質改善活動を行いつつ、特性検査や独自のスクリーニングを実施しています。また、設計開発段階から信頼性の作り込みを推進し、信頼性確保に向けた信頼性設計や設計審査などの活動と信頼性試験による検証を行っています。
摩耗故障
図1の(3)の領域は摩耗故障期間と呼ばれ、この期間に発生する故障を摩耗故障といいます。摩耗故障は、基本的な構造や材料に起因する摩耗や劣化によるもので、この期間で特定の故障が集中的に発生して、故障率は指数関数的に増加し始めます。アルミ電解コンデンサの場合は、実使用時の環境温度や自己発熱によって電解液が蒸発して(ドライアップ)、静電容量の減少、tanδ や漏れ電流の増加などの等の故障が発生します。ただし摩耗故障は、事前の予知による交換などで予防できます。
偶発故障と故障率
前述の議論から、初期故障は品質管理に起因し、摩耗故障は固有技術や設計上の問題と考えることができます。一方で、機器やコンデンサを含むデバイスが実際に使われる期間にも故障が発生します。すなわち初期故障にも摩耗故障にも該当しない故障です。この故障はランダムに発生し故障率は一定です。この期間を偶発故障期間、発生する故障を偶発故障とよびます。ただし故障率が一定というだけでゼロではありません。ある確率で故障は起こるがその確率は一定であるという意味です。サイコロを投げて、1の目が出るのは偶発的ですが、その確率は一定であることと同じです。
偶発故障期間の故障率には「平均故障率」と「瞬間故障率」があり、偶発故障での故障率と寿命予測は信頼性工学の対象となります*02。
*02 偶発故障が発生する主な要因には、異常な電圧や過大な突入電流などの電気的なオーバーストレスや、機械的・物理的ストレスなどがあります。ただし仕様を越えた特殊な条件下で使用されない限り、期待寿命は充分に長く、実使用では摩耗故障に至らないように設計されています。
平均故障率
平均故障率は「総故障数を総稼動時間で割った値」で、コンデンサでは、%/1,000h、ppm/1000h 等の単位が一般的に用いられています。また故障率が⼩さい部品などでは、1つの対象物が109時間作業する間に発生する故障の数で表します。単位はFIT(Failure In Time)で、1FITは=10-9/時間です式(01) *03 。
*03 稼働10億(109)時間あたりの平均故障回数。半導体部品など、大量に生産され故障率が極めて低い工業製品についてよく用いられる。

ここで注意したいことは平均故障率の解釈です。たとえば、平均故障率300FITは 300×10-9、すなわち 3×10-7です。これは稼働試料数と稼働時間の積が107(1000万時間・個)で 3個の故障が発生するということです。個々の製品そのものの寿命が107時間という意味ではありません。
瞬間故障率と寿命推定
瞬間故障率は、それまで生存してきた部品やユニットが、時間 t に故障する確率です。この値は、時刻 t と t+ΔT の間にある期間で単位時間あたりに故障する製品数と言うこともできます。⼀般に故障率という場合は「瞬間故障率」を指します。
瞬間故障率の確率密度が指数関数であると*04、故障率はχ2分布(カイ二乗分布)に従うとされています*05 。数百から数千時間の高温連続通電試験を行い、試験結果を χ2分布で解析することにより上限区間推定故障数Nを求める手法があります*06, 07 。
具体的には、ある条件下で試験した時間 t における累積不良確率Ftは、信頼性水準R(%)、有意水準α (1-R, %) 、故障数 r に依存する自由度 β を用いた以下の式で表すことができます*08 。

*04 https://bellcurve.jp/statistics/course/8009.htmlz
*05 瀬戸谷 孝, “半導体LSI の信頼性予測・推定の実際” REAJ誌 2018 Vol.40, №6(通巻244号)
*06 鈴木他,”信頼性データ解析”,日科技連出版(2009)
*07 JEDEC JESD-47
*08 JEITA EDR-4708B:信頼性集積回路の半導体認定ガイドライン
期待寿命は時間依存性を持つ瞬間故障率Ftの逆数と考えることができるので、式(02) の逆数の式(03)から期待寿命Lestimateを求めることができます。
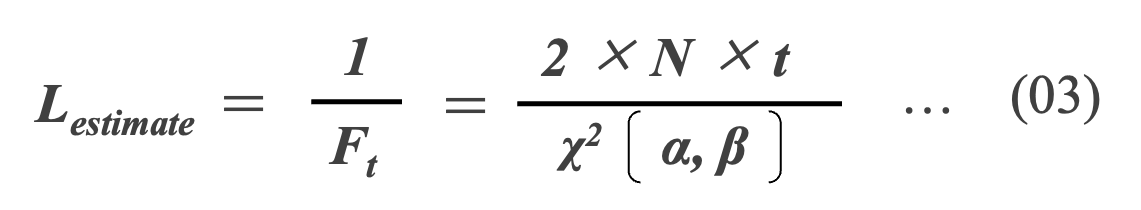
たとえば、50個のコンデンサをある条件で試験したときに、1000時間の間に1個故障したとし(r = 1)、信頼水準を95%(有意水準α=5%)*09で寿命を推定すると、期待寿命の下限 Lshortおよび上限 Llongは、以下のように計算できます。
*09 信頼水準95%とは、100回試行したら95回は適合することを意味します。


コンデンサを使う上では寿命の下限が重要となるので、この場合の期待寿命は約1年となります。
試験で故障が発生しなかったときの寿命推定と故障率
初期故障が取り除かれた製品から偶発故障を検出することは困難です。仕様範囲内の条件で試験を行っても、故障は発生しにくいからです。したがって試験で故障が発生しなかった場合は期待寿命の上限を求めることはできません。この場合には式(04)の分母のα/2がαとして、期待寿命の下限 Lshortを以下のように計算します。

式(06)は、試験で故障が発見できなくとも寿命を推定することは可能であることを示しています。ただし実際の使用では、温度や電圧などの条件が、試験条件よりも緩和されている場合が多いため、試験からで得られた期待寿命は、次章で述べる手法で補正することができます。
前述したように期待寿命と故障率は互いの逆数です。このため、式(06)の逆数は故障率の上限になり、その値は約0.06%/1000時間となります 。
劣化による交換が行われない限りコンデンサの期待寿命は、故障までの平均時間MTTF(Mean Time To Failure)と考えて差し支えありません。
コンデンサの故障率に影響する因子
コンデンサの寿命や故障率には様々な要因が影響します。たとえばMIL-HDBK-271F-Notice2 第10章ではアルミ電解コンデンサの故障率λPを以下の式で定義しています。これらの因子のうちで、温度・電圧はコンデンサの寿命に大きく影響します。このためコンデンサを使う上で適切なディレーティングを想定することで推定寿命を伸ばすことが可能になります。
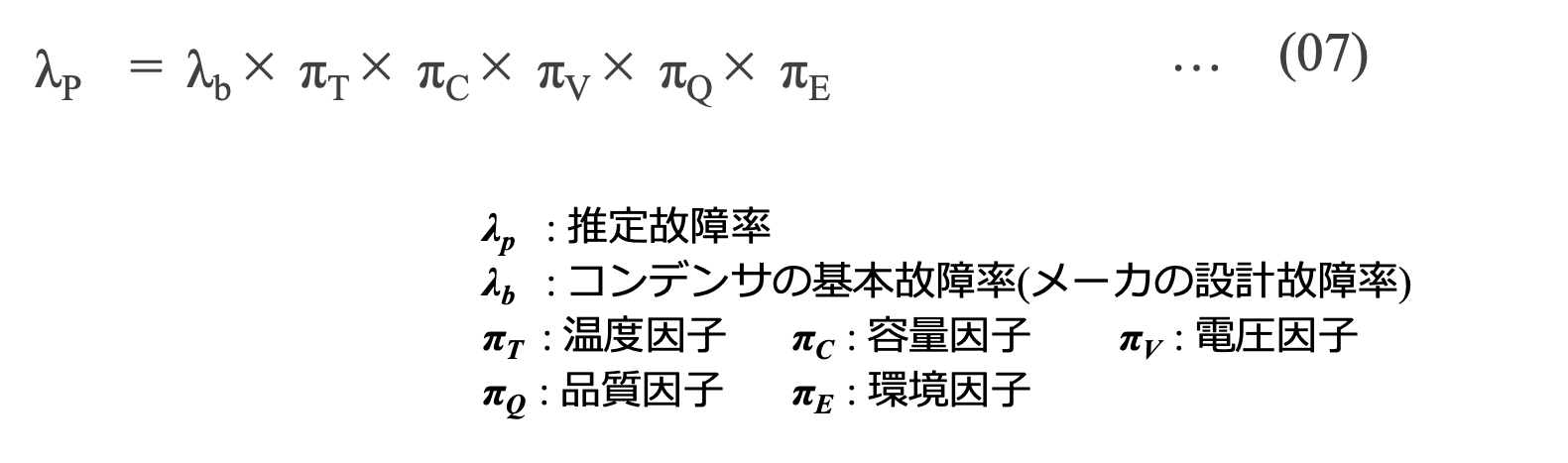
コンデンサの一般的な寿命推定式
故障率の逆数が寿命です。コンデンサの寿命予測には寿命推定式が使われます。計算式はメーカごとに異なり、コンデンサの構造や設計によって理論的な関係と経験的な関係の両方が考慮されます。一般的にコンデンサの寿命は、動作温度、印加電圧、リプル電流が寿命の要因になります。その一般式は各要因の加速係数を考慮した式(08)で表されます*10。

*10 A. Albertsen, ”Electrolytic capacitor lifetime estimation,“ Jianghai Europe GmbH, Tech. Rep., 2010. [40]
式(08)の各加速係数は、コンデンサの種類に固有の値を取ります。このため以下の項では、Al-Ecap、MF-cap、MLCCの寿命推定式について考察します。
アルミ電解コンデンサ(Al-Ecap)の寿命推定
ほとんどのAl-Ecapの定格寿命L0は、1,000~15,000時間(0.11~1.71年)です。ただし定格寿命は、温度、印加電圧、リプル電流によって変わり、寿命予測と加速係数はメーカによって異なっています。
この理由は、メーカによって電解液の化学的性質やコンデンサのトポロジーが異なるだけでなく、試験方法も異なる可能性があるためです。しかも、ほとんどの寿命予測と加速率の計算式は、基礎理論から導き出されたものではなく、実験データに合わせて経験的に導き出されたものです。このため、あるメーカの加速率を別のメーカに適用する際には注意が必要です。本項では、Al-Ecapの寿命と温度・電圧・リプル電流との基本的な関係を概説し、寿命を推定するためのポイントを概説します。
温度による影響(温度加速 KTと10℃2倍則)
Al-Ecapの静電容量やtanδは、温度影響を大きく受けるパラメータです。とくに高温では静電容量の減少やtanδの増大が速く進みます。これは主に電解液が電極反応してガスを発生し、封口ゴムを通して外部へ拡散することにより電解液が減少するためです。すなわち化学反応がAl-Ecapの寿命に影響しています。このため、ほとんどの研究者やメーカは、コンデンサの寿命がアレニウスの法則に従って温度の影響を受けると仮定しています。式(09)に示したアレニウス方程式は、反応速度k と温度の関係を示す一般的な方程式です。

式(09)の対数を取り、反応速度の逆数を寿命Lと考えると、寿命と温度との関係は式(10)で表すことができます。
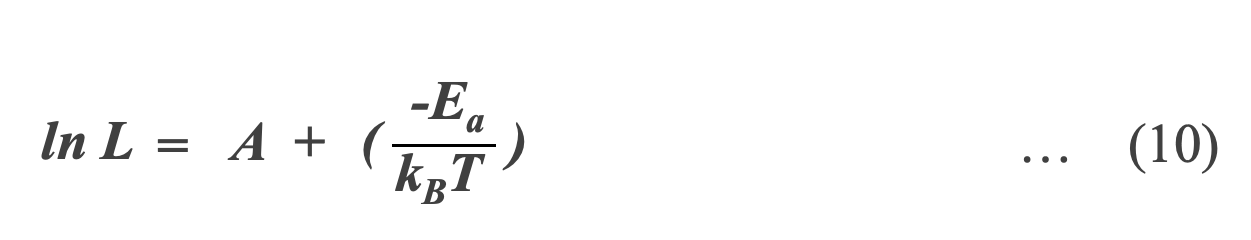
温度T1における寿命L1と、 T1 よりも高温のT2 における寿命L2 との比は、式(11)で求められます。
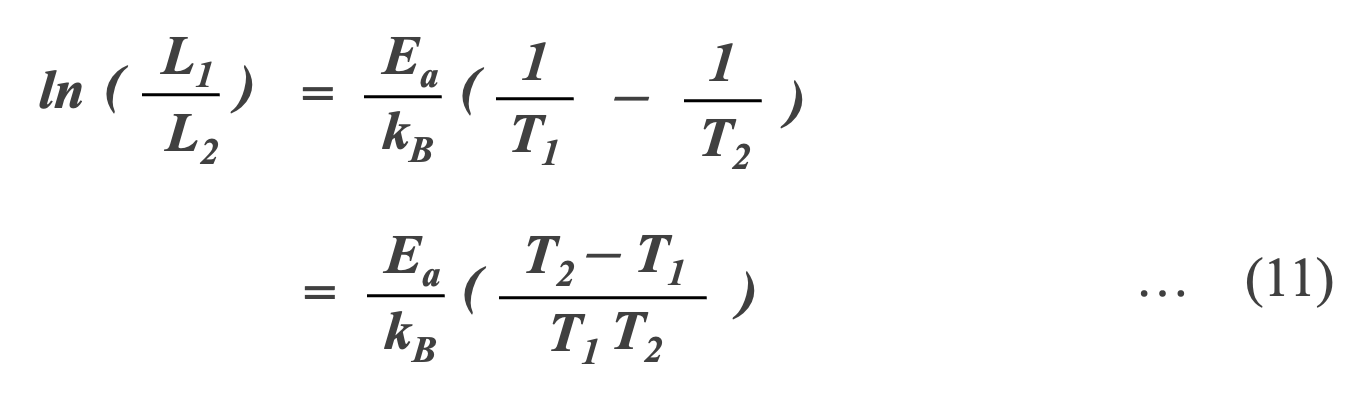
Al-Ecapの故障を誘電体の酸化アルミニウムの還元酸化反応と考え、式(11)の活性化エネルギーEaを酸化アルミニウムの活性化エネルギーの 1.506×10-19J(0.94eV)とすると*11、式(11)は以下のようになります。
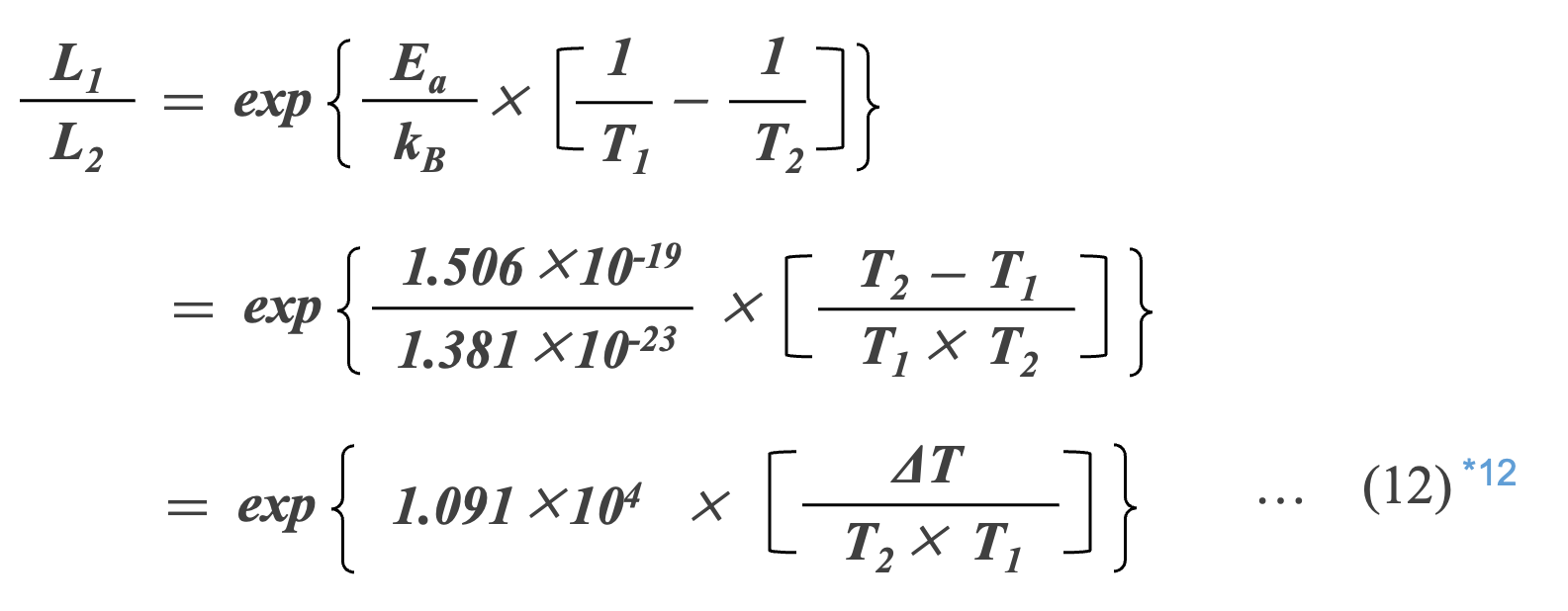
*11 H. Ma and L. Wang, “Fault diagnosis and failure prediction of aluminum electrolytic capacitors in power electronic converters," in 31st Annual Conference of IEEE Indus-trial Electronics Society, 2005 (IECON 2005), 2005, pp. 842{847.[42]
*12 T2 – T1 = ΔTと置いています。
最高使用温度(カテゴリー上限温度)が105℃のAl-Ecapを。周囲温度が95℃で使用したときの寿命L95と105℃の寿命L105との寿命の比は、式(13)のように計算できます*13。
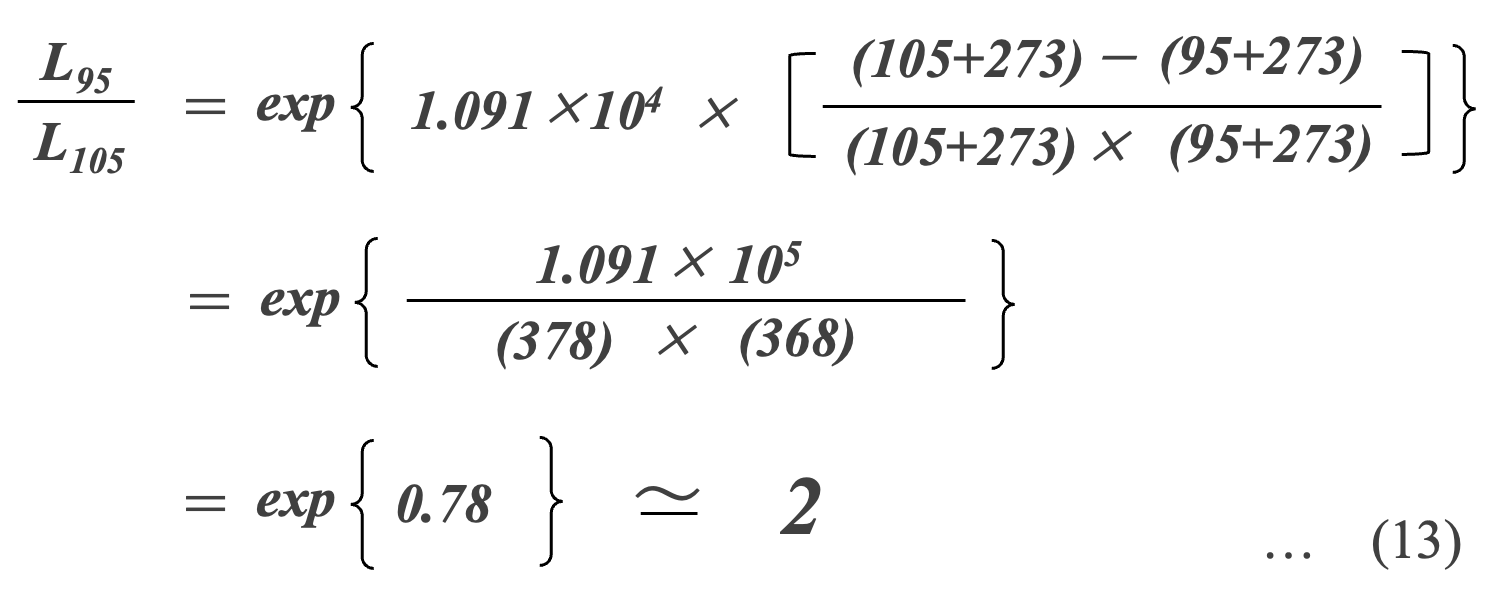
*13 P. Venet, et. al., ” Influence of aging on electrolytic capacitors function in static converters: Fault prediction method," European Physical Journal-Applied Physics, vol. 5, no. 1, pp. 71{83, 1999.[105]
式(13)の計算結果は、温度95℃の寿命L95は105℃の寿命L105の約2倍と推定されることを示しています。すなわち『動作温度が10℃低くなるごとにコンデンサの寿命は2倍に延びる』という意味です。これは、寿命の温度加速を示す経験則であり、いわゆる「10℃2倍則」として知られています。式(12)を一般化した式(14)を温度加速KT-ELとしています*14 。

*14 より小型のコンデンサでは、電解液に依存する温度加速係数KTに支配されます。
ただし「10℃2倍則」を適用する際には注意が必要です。式(13)は、カテゴリー上限温度と動作温度の積を「378×368」(= 1.391×105)と仮定していますが、低温の場合には寿命を10~40%過小評価する可能性があります*15。たとえば、50℃での寿命L50と60℃の寿命L60 との比を式(15) で計算すると、95℃/105℃の場合より大きな値となり、この温度で「10℃2倍則」を適用すると寿命を約38%過小評価していることがわかります。
*15 S. Parler Jr, \Selecting and applying aluminum electrolytic capacitors for inverter applications," Cornell-Dublier, Tech. Rep., 2010. [106]
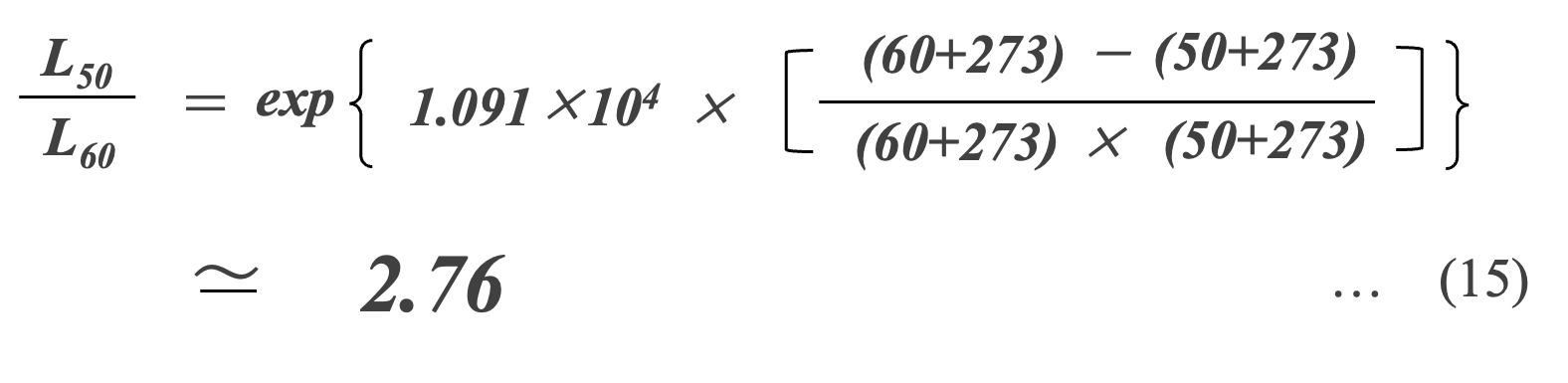
電圧による影響(電圧加速 KV)
電圧が寿命に及ぼす影響を表す電圧加速KVの経験的モデルとして広く使われているのは式(16)で、主に中型から大型のコンデンサに使用されています。高い電圧を印加してコンデンサを使用すると、誘電体へのストレスが大きくなって寿命が短くなり、定格電圧に対する余裕度が大きいほど、誘電体層へのストレスが減少して、誘電体のヒーリングが促進される*16ため、寿命が大幅に延びる可能性があります。式(16)の乗数 n はメーカ、定格電圧、容量の大きさ、コンデンサのサイズなどによって異なり、一般的には、2~5値が使われています*17。
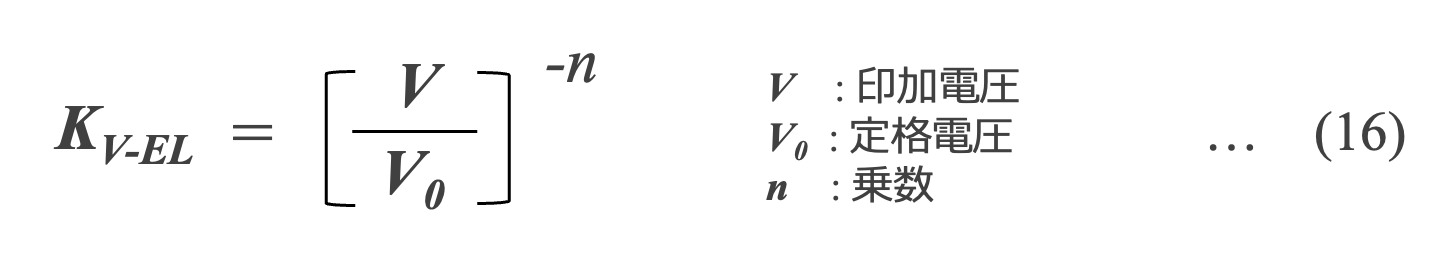
*16 S. Parler Jr, “Deriving life multipliers for electrolytic capacitors," IEEE Power Electronics Society Newsletter, vol. 16, no. 1, pp. 11{12, 2004. [116]
*17 https://www.jstage.jst.go.jp/article/ieejjournal1888/95/5/95_5_384/_pdf/-char/ja 電気学会誌 絶縁体に対する電圧の影響を示す経験則に由来しています。
リプル電流による影響(リプル加速 KR)
コンデンサにリプル電流が流れると、コンデンサの内部温度が上昇して、周囲温度、コンデンサ表面温度、内部中心部温度がすべて大きく異なる可能性があります*18, 19。Al-Ecapの劣化故障は、一般に電解液中の溶媒の蒸発が原因であると考えられています。電解液の代表的な溶媒であるエチレングリコールの蒸気圧は、コンデンサの動作温度の範囲内で何桁も変化する可能性があります。またコンデンサの構造によっては、溶媒は高温で容易に蒸発し、導電性を失うため、Al-EcapのESRを増加させます。このためコンデンサの寿命予測をするには、周囲温度を考慮した温度加速KTだけでなく、リプル電流による内部温度の上昇を考慮したリプル加速係数KR を考慮する必要があります。
*18 M. L. Gasperi, \Life prediction model for aluminum electrolytic capacitors," in Conference Record of the 1996 IEEE Industry Applications Conference (IAS 1996), 1996, pp. 1347{1351. [88]
*19 G. Rhoads and A. Smith, “Expected life of capacitors with non-solid electrolyte," in IEEE 34th Electronic Component Conference, 1984, p. 156. [107]
リプル電流によるコンデンサの発熱と中心部温度
コンデンサにはリプル電流を除去して平滑化する役割があります。図2に示したようにコンデンサにリプル電流が流れると、ジュール熱が発生してコンデンサが発熱します。
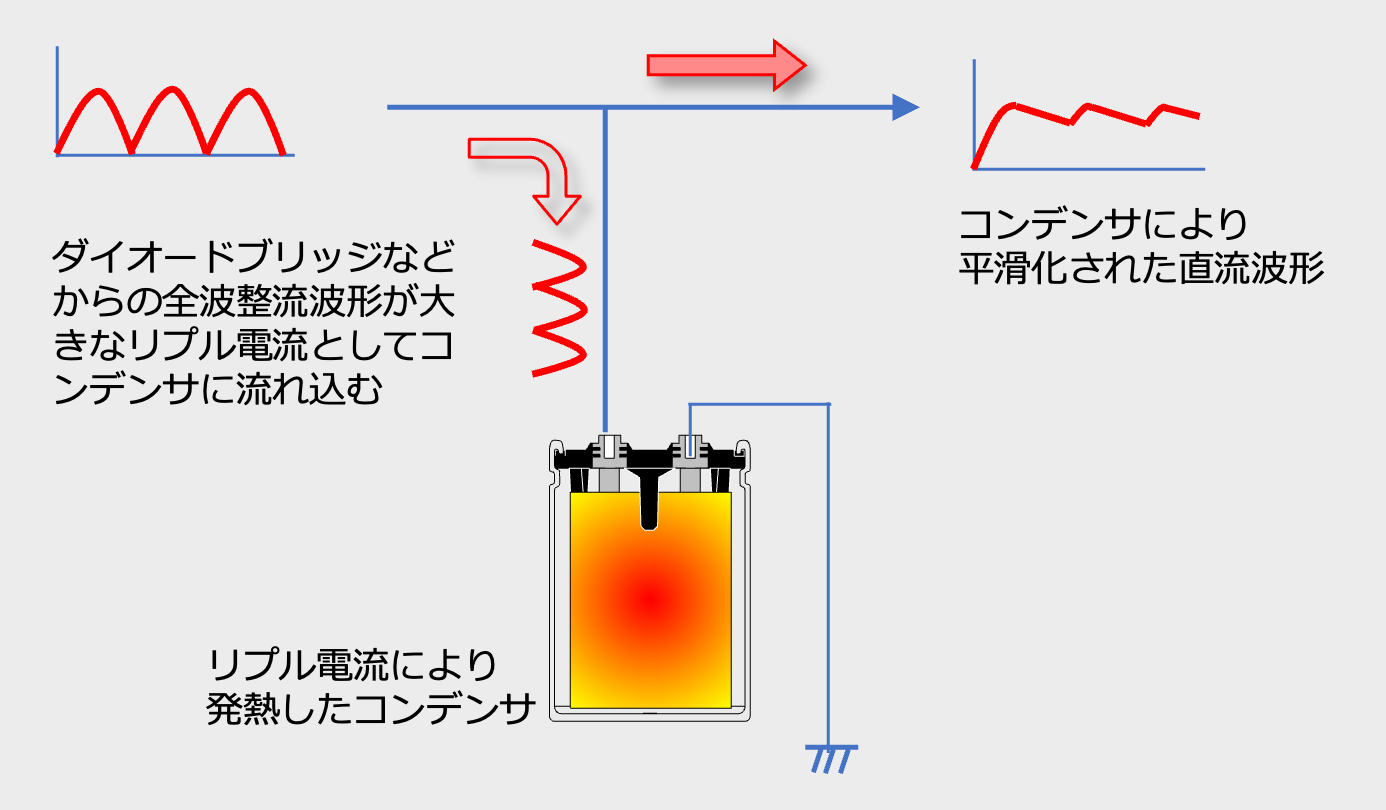
コンデンサによるリプル電流の除去とコンデンサの発熱のイメージ図
発熱によってコンデンサ内部の温度が上昇します。その温度上昇ΔTは、熱抵抗Rthを持つ素子が消費する電力(P)から計算できます(式(17))。電力(P)は、等価直列抵抗(ESR)にを持つコンデンサにリプル電流が流れることによる発熱でコンデンサ全体に散逸します。

*20 当社では簡易的に以下の式を適用する場合があります。
リプル電流にはさまざまな周波数があります。ESRは周波数によって変化するため、式(17)は周波数の関数として取り扱う必要があります。さらにESRは温度によっても変化します。このため、リプル電流によるコンデンサの中心温度(中心部温度)Tcは、周囲温度Ta とESRの周波数特性および温度特性を考慮した式(18)で表されます。

リプル電流加速KRの要素
① 温度の計測
リプル電流による寿命への影響を見積るには、周囲温度Taやコンデンサ表面温度Tsだけでなく、前述のコンデンサの中心部温度Tcが必要になります。Ta とTs は比較的簡単に測定できますが、コンデンサが動作しているときにTcを直接測定すること難しいかもしれません。
ネジ端子形や大型のスナップイン形のAl-Ecapでは、メーカがコンデンサ内部に熱電対を組み込んだユニットを提供することがあります。しかしこの手法をリード線形などの小型コンデンサに適用するのは困難であるため、通常は表面温度で代用するか、表面温度から中心部温度を概算しています
② ESRの温度特性と周波数特性
Al-EcapのESRは一定ではなく、コンデンサ内部の温度と周波数に依存します(図3)。
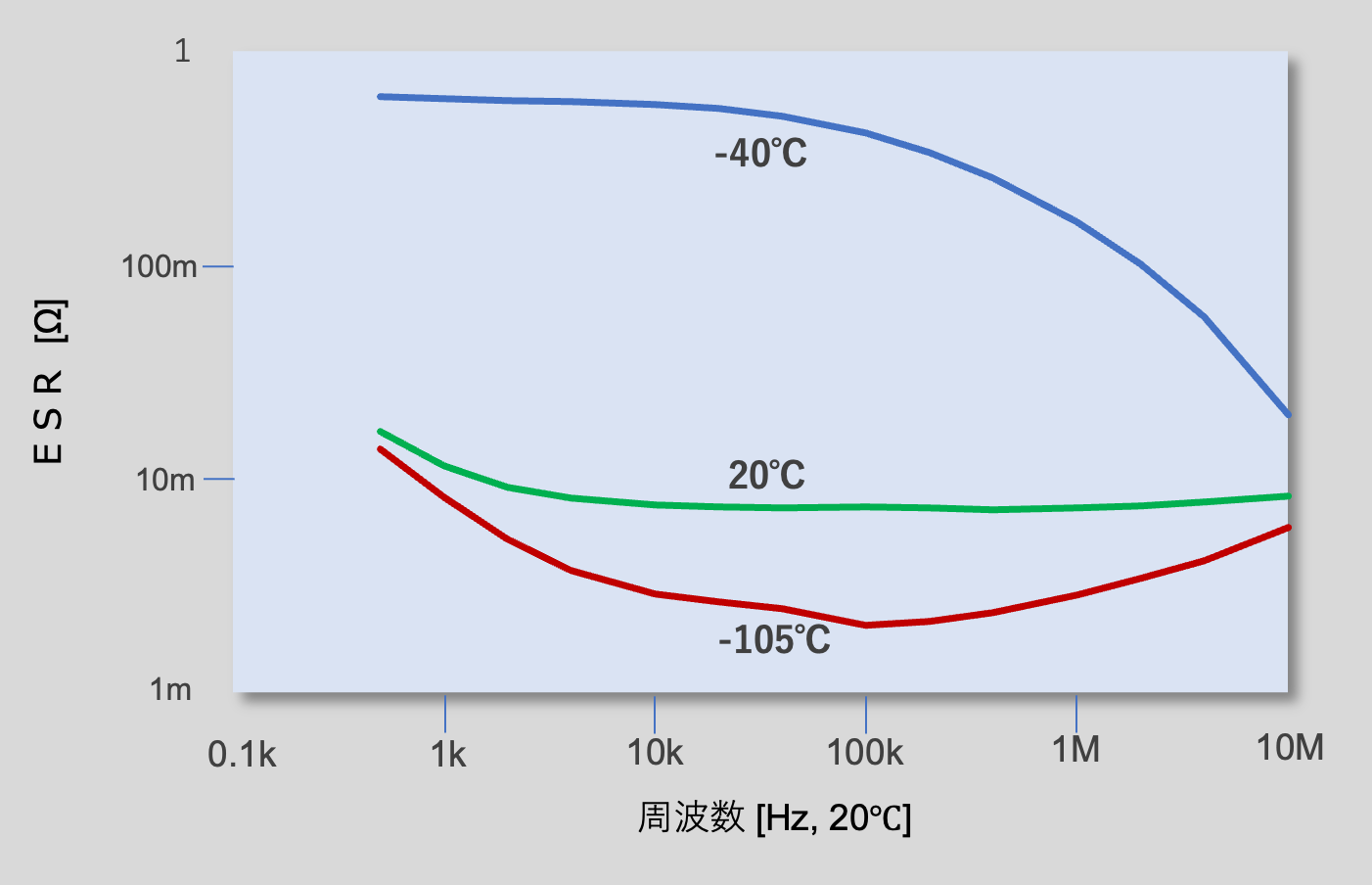
Al-EcapのESRの温度特性・周波数特性
(当社 VGR形 定格400V 4700μF)
ESRを構成する要素は、誘電体損失の周波数依存性に起因する成分の抵抗(Rf)、電極箔、リードタブ、電解液や他のコンデンサ構成部品に起因する抵抗(Rc)、および温度による電解液の粘度の変化に起因する抵抗(RT)の3つの成分から構成されます。 これを式で表すと式(19) の様になります*21。

*21 F. Hayatee, “The equivalent series resistance in electrolytic capacitors," Electrocomponent Science and Technology, vol. 2, pp. 67-72, 1975. [111]
*22 Rf は、電圧反転時に誘電体酸化物中の双極子が整列することに起因する抵抗です。
M. L. Gasperi, \A method for predicting the expected life of bus capacitors," in Conference Record of the 1997 IEEE Industry Applications Conference (IAS 1997), 1997,pp. 1042-1047. [112]
Al-Ecapの電解液の粘度と導電率はESRに大きく影響します*23 。電解液の粘度が低いほど陽極や電解紙に浸透しやすくなって導電性が高まり、ESRが小さくなります。電解液の粘度と導電率は温度依存性が大きく、低温では粘度が高くなり導電性が低下してESRが大きくなります。電解液の導電率は、電解液の溶媒と溶質のイオン半径にもよりますが、ESRが室温の10倍から100倍程度大きくなる場合があります。
RT に含まれるESRの温度依存性は式(20)で表され、電解液の粘度変化に起因する抵抗です。この粘度の変化はイオン移動度と電解質抵抗を変化させます*24

*23 電解液の導電率は濃度と粘度で決まります。溶解度 が大きく電離度が大きい電解質では電荷密度が大きくなります。粘度 η 〔Pa・s〕が小さい溶媒とイオン半径が小さい電解液では移動度 μ 〔m2/V・s〕が大きくなります。
*24 Determining End-of-life, ESR, and Lifetime Calculations for Electrolytic Capacitors at Higher Temperatures, Aug. 2008. [113]
③ コンデンサの熱抵抗 Rth
リプル電圧加速係数を計算するのに必要な最後の要素は、コンデンサの熱抵抗 Rth です。 Rth は熱の伝えにくさ示す数値で、 Rthが小さいほどコンデンサ内部の熱が外部に放散しやすいことを意味します。 Rth は全熱伝達係数 Htotalとコンデンサの表面積 A の逆数です(式(21))。

熱伝達は図4に示す対流(convection)、輻射(radiation)、伝導(conduction)の3つの異なる放熱モードで構成されるため、全熱伝達係数 Htotalはそれぞれの熱伝達係数の和になります(式(22))。

対流は周囲の空気の動きによって放散される熱、輻射は熱の放出によって放散されるエネルギー、伝導は固体との接触を通じて放散されるエネルギーです(図4)。リプル電流によって発生したコンデンサの熱に大きく影響するのは、対流と輻射です。このため式(22)のHconvectionとHradiationを見積ることが重要です。
Hconvectionの主な要因には、コンデンサの数(実装密度)と径、空冷の風速、表面温度Tsと外気温度Taなどがあります。Hradiationの主な要因には、表面温度Tsと外気温度Ta、コンデンサ筐体の表面積および放射率(emissivity)が挙げられます。
以上のことから、リプル電流によるコンデンサの発熱と寿命に対する影響をより精密に推定するには、
・ESRの周波数依存性と温度依存性
・熱抵抗(Rth)
・対流と輻射の熱伝達係数( HconvectionとHradiation)
等を把握する必要があります。
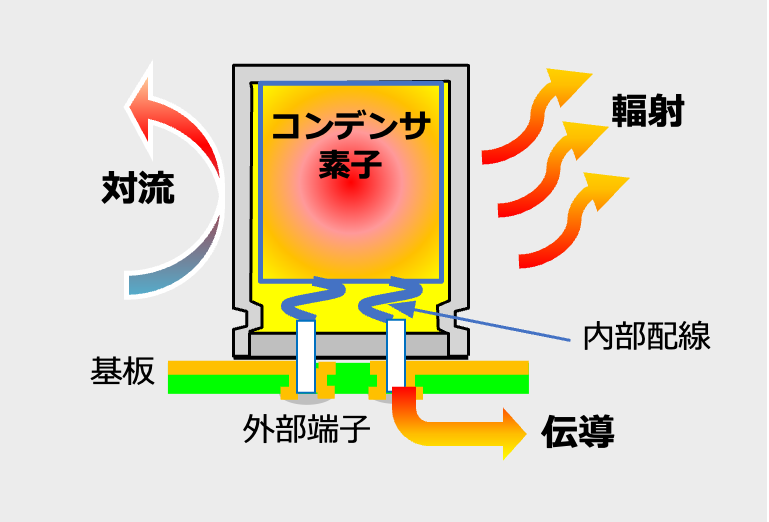
Al-Ecap の対流、放射、伝導による放熱のイメージ
Al-Ecapの寿命推定式
これまでの議論から、温度、電圧、リプル電流の各因子がAl-Ecapの寿命に及ぼす効果を考慮すると、以下の式(23)を考えることができます。
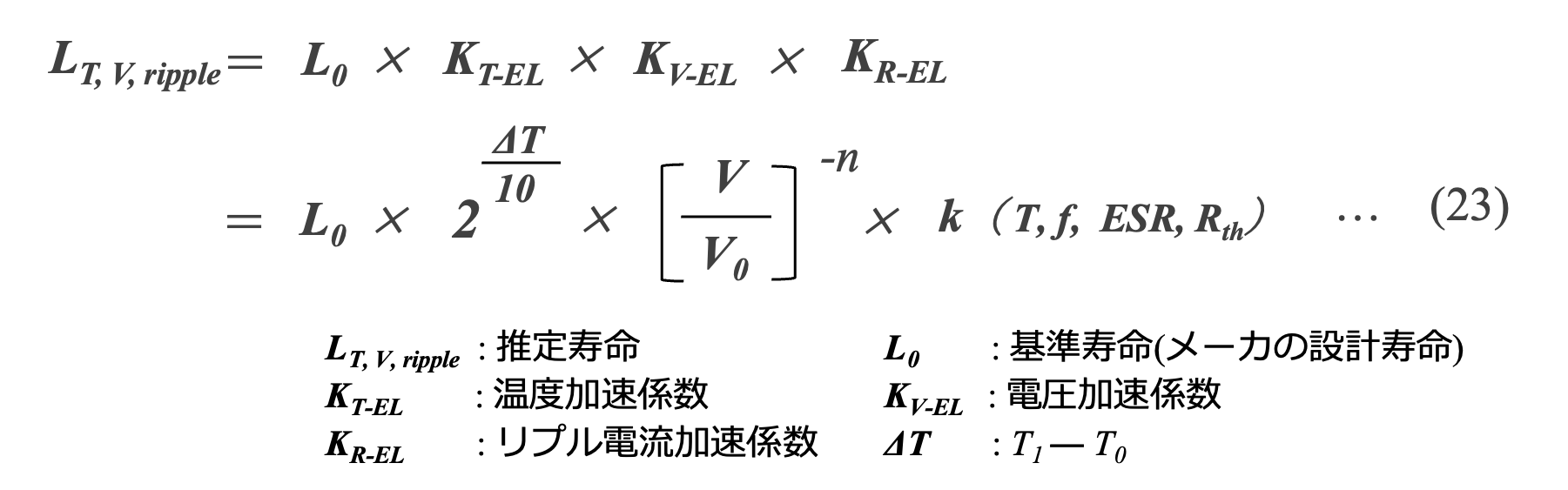
当社では、KT-ELに温度の10℃2倍則、 KV-ELに電圧の2.5乗則を使った式(24)を標準としています。なお、リプル電流による温度上昇は、ΔTに含めています。
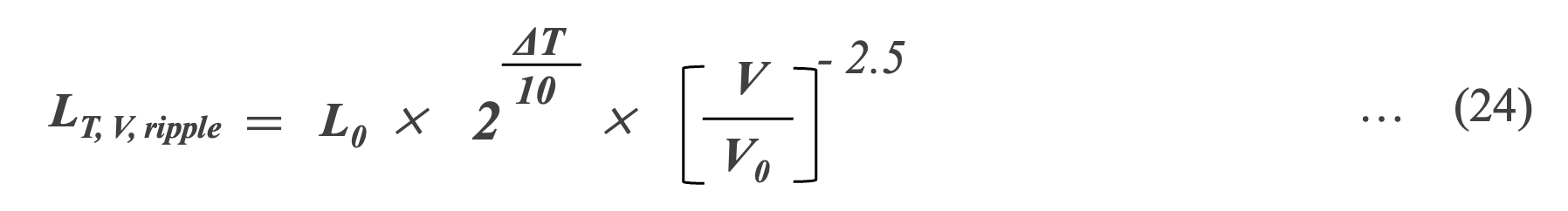
蒸着電極形フィルムコンデンサ(MF-cap)の寿命推定
MF-capの寿命予測を行う場合には、電圧と温度の加速条件で2,000〜3,000時間程度の試験を行い、その結果をもとにして動作条件を少し下回る条件(ディレーティング)で動作させたさせたときの寿命を算出しています。各メーカはそれを概ね10万~15万時間程度(約11~15年)の期待寿命として公開しています*25。すなわち、ほとんどの寿命予測と加速率の計算式は、基礎理論から導き出されたものではなく、各メーカは実験データに合わせて経験的に導き出されたものです。さらにMF-capには他のコンデンサにはない自己回復性(SH)があり、その性能はメーカによって異なります。このため、あるメーカの加速率を別のメーカに適用する際には注意が必要です。
前述したようにMF-capの一般的な故障モードは、多数の小さなSHによる容量の減少です。この事象の発生数は時間とともに増加し*26、容量減少の変化率は、温度、電圧、湿度に依存します。このため、これらのパラメータがMFCの寿命に影響する加速因子になります。本項では、これらの加速因子と加速係数の考え方をご説明します。
*25 “Capacitors Age and Capacitors Have an End of Life," Emerson Network Power, Tech. Rep., Aug. 2008. [117]
*26 J. Zhao and F. Liu, “Reliability assessment of the metallized film capacitors from degradation data," Microelectronics and Reliability, vol. 47, no. 2-3, pp. 434{436, Feb.2007. [65]
温度による影響(温度加速KT-MFC)
Al-Ecapと同様にMF-capにおいても温度が上がるほど寿命は短くなり、寿命の温度依存性はアレニウス則に従うことが示されています*27(式25)。
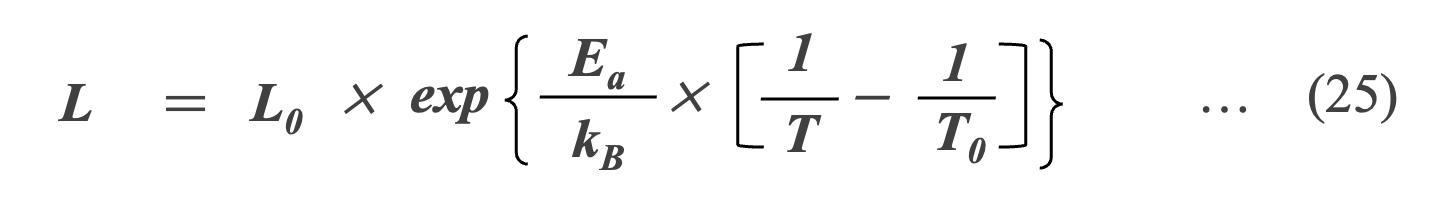
*27 Q. Sun, et. al, “Reliability assessment of metallized film capacitors using reduced degradation test sample,” J. Qual. Eng. Int., vol. 29, no. 2, pp. 259–265, Mar. 2013. [14]
アレニウス則から導かれる加速係数 KT-MFCは、「10℃2倍則」が使われますが、定格温度を8℃超えるごとに寿命が半分になるとする「8℃2倍則」を提案する説もあります(式(26)) *28。

*28 W. Sarjeant, J. Zirnheld, and F. MacDougall, “Capacitors," IEEE Transactions on Plasma Science, vol. 26, no. 5, pp. 1368{1392, 1998. [39]
電圧による影響(電圧加速KV-MFC)
MF-capを定電圧モードで動作させるとSHが常に発生するため静電容量は着実に低下します。このためパルス電圧モードでは長寿命であっても、定電圧条件下では寿命が短くなることが報告されています*29, 30。
印加する直流電圧が定格電圧に近いほど寿命が短くなるため、寿命計算には何らかの電圧加速を含める必要があります。コンデンサの品質、製造方法、およびタイプによって異なりますが、この加速係数KV-MFCは式(27)で表され、nは通常10~20の範囲にあります*30, 31。この非常に大きな電圧加速係数は、過電圧がコンデンサの寿命に劇的な悪影響を及ぼす可能性があり、MF-capの定格電圧は極めて重要であることを意味します。

*29 H. Fuhrmann, et al., ”Novel Measurement Methods for In-depth Analysis of AC Metallized Film Capacitors," in IEEE International Symposium on Electrical Insulation, 2004, pp. 568-571. [119]
*30 W. Sarjeant, et al., “Energy storage capacitors: Aging, and diagnostic approaches for life validation," in IEEE Transactions on Magnetics. Aerovox Inc, New Bedford, Ma, 1997, pp. 501-506. [91]
*31 T. Umemura, et al., “Accelerated-life Testing of Power Capacitor Dielectric Systems," IEEE Transactions on Electrical Insulation,, no. 3, pp. 309-316, 1987.[121]
湿度による影響(電圧加速KRH-MFC)
プラスチックフィルムには水分を透過したり吸収する性質があります。MF-capの内部に残続したり、外部から侵入した水分は、フィルムの絶縁性を低下させ、通常厚さ20~100nm以下の蒸着電極の脱離や腐食を発生させます。また誘電体フィルム中の水分は、水分子の双極子によって損失係数を増加させ、絶縁抵抗が低下し、最終的には破局的な故障につながります*32。また電圧を印加すると、水分と蒸着金属が電気化学反応を起こすことでガス発生や絶縁化が発生し(式(28) *33)、故障に至ります。
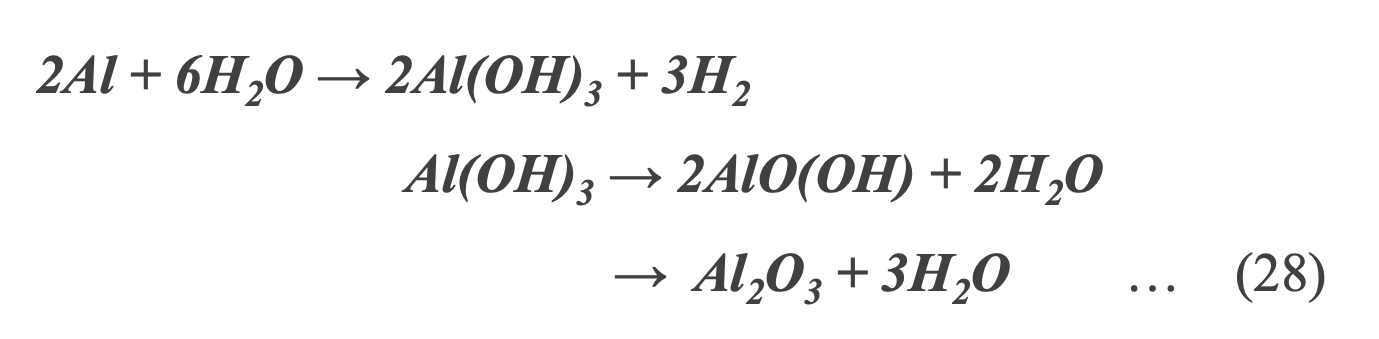
*32 Brown R. W. “Linking Corrosion and Catastrophic Failure in Low-Power Metallized Polypropylene Capacitors.” IEEE Transactions on Device and Materials Reliability Vol. 6 No. 2 (2006): pp. 326-333. [17]
*33 高温高湿バイアス下でのアルミ蒸着電極の陽極酸化反応
図5は、高温高湿バイアス試験で故障したフィルムコンデンサの外観(左)とX線CT画像(右)です。電流と水分によって蒸着電極が腐食し、フィルムが分解してガスが発生しました。発生したガスの圧力によって樹脂ケースが膨らみ、コンデンサの巻回素子の外層部分が、損傷している様子が観察されました。

高温高湿バイアス試験で故障したフィルムコンデンサ*の外観(左)とX線CT画像(右)
*当社 MKCP4形700V 80μF
Zhuaiらは、MF-capの相対湿度に対する容量変化の変化の大きさを評価し、湿度加速について言及しています(図6)*34。
*34 Shuai Zhao a, Shaowei Chen b, Huai Wang, “Degradation modeling for reliability estimation of DC film capacitors subject to humidity acceleration” Microelectronics Reliability Vol 100–101, September 2019, 113401
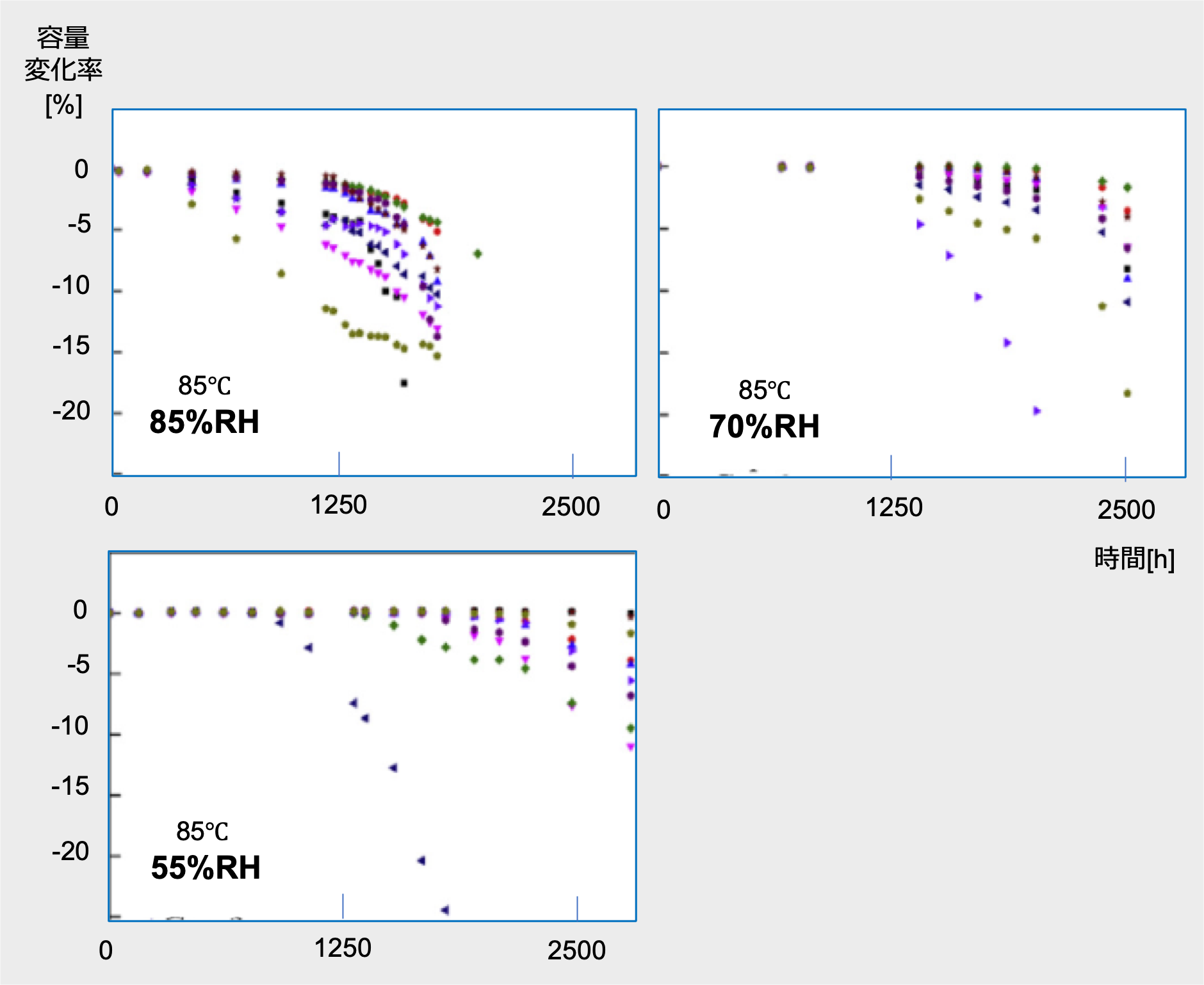
MF-capの高温高湿バイアス試験における容量変化
(樹脂ケース形1100V 40μF)
湿度が寿命に及ぼす影響は、Hallberg-Peck則と呼ばれる式(29)を使用して推定できます*35。ここで RH0は基準湿度です。
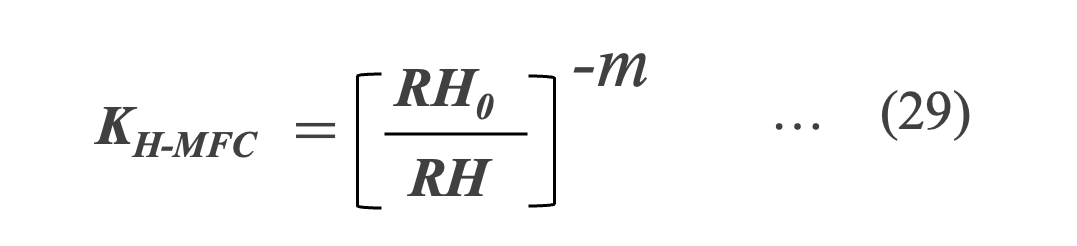
*35 Ö. Hallberg and D.S. Peck, Qual. Reliab. Eng. Int. 7 (1991) 169.
Taiらは、MF-capの高温高湿条件下での加速エージング試験と故障メカニズム解析から、高湿度(相対湿度69%以上)の使用環境下では、水分子と酸素が電気化学的腐食を引き起こし、コンデンサフィルム上のアルミニウムや亜鉛等からなる蒸着金属を損傷させることを実証しています。さらに寿命推定モデルを確立し、故障の活性化エネルギーEa = 1.48eV、湿度故障の係数mを4と算出しています*36 。MF-capの耐湿性の向上は、同コンデンサの用途を拡大するキーポイントです。近年では、85℃85%バイアス負荷1000時間(THB : Thermal Humidity Bias Test *37 )を保証する製品も開発されています。
*36 https://www.sciencedirect.com/science/article/abs/pii/S0026271422002797
*37 Thermal Humidity Bias Test
温度、電圧で注意すべきこと
Al-Ecapと同様にMF-capに流れるリプル電流はMF-capの中心部温度を上昇させます。中心部温度TCは、周囲温度Ta, 誘電損失Pd, 熱損失Ptおよびコンデンサの熱抵抗Rthを用いた式(30)で近似できます。 TC はMF-capの寿命に直結しますので、 TC は定格温度よりも低く設定することが必要です。
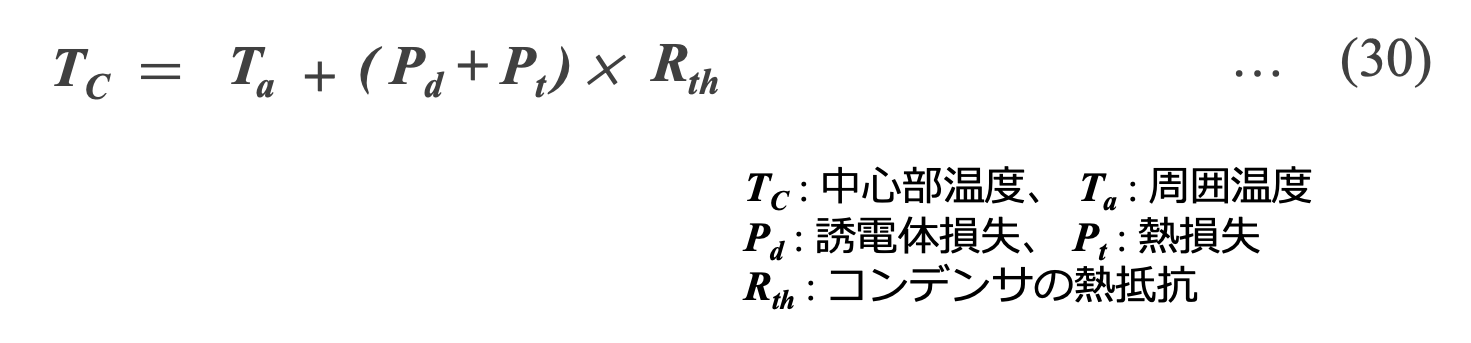
誘電損失Pdは、周波数 f における双極子の再配列によるフィルムポリマーのエネルギー吸収に起因し、以下の式(31)で表されます。
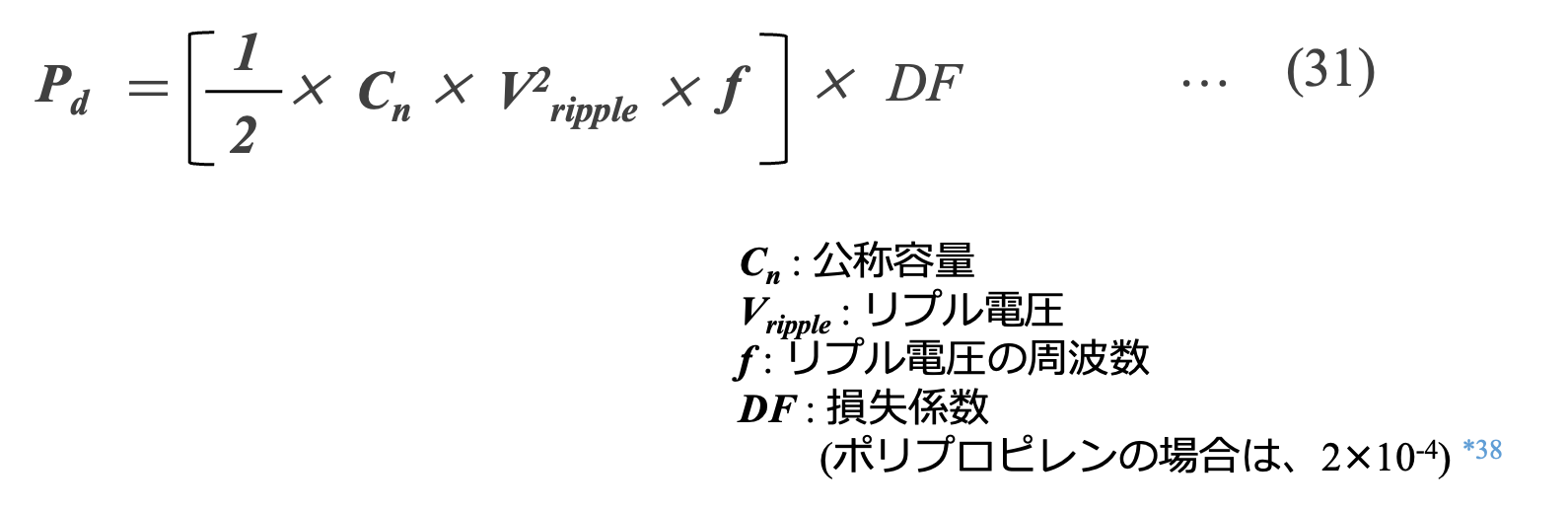
*38 G. Buiatti, S. Cruz, and A. Cardoso, “Lifetime of film capacitors in single-phase regenerative induction motor drives," IEEE International Symposium on Diagnostics for Electric Machines, Power Electronics and Drives, 2007 (SDEMPED 2007), pp.356-362, 2007. [66]
また熱損失Ptはリプル電流によるコンデンサのジュール熱として式(32)で表されます。

動作電圧VWは、直流電圧とリップル電圧の和であることから、式(33)のようになります。MF-capを使用するときには、動作電圧より高い定格電圧を持つものを選ばなくてはなりません。

MF-capの寿命推定式
これまでの議論から、温度、電圧、湿度の因子がMFCの寿命に及ぼす効果を考慮した以下の式(34)を考えることができます。
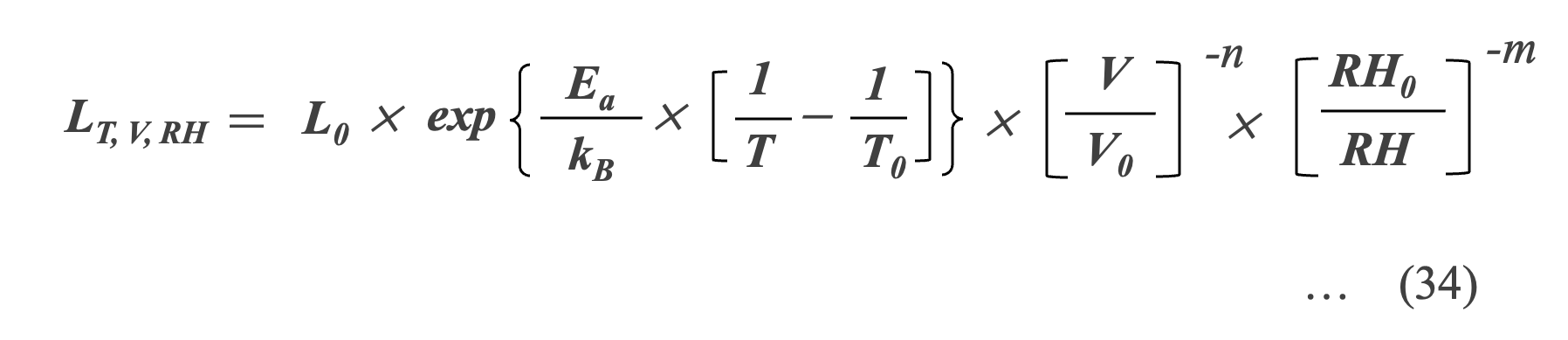
この式を用いるためには、故障の温度依存性に関する活性化エネルギー Ea 、電圧加速係数 n、湿度の加速係数 m を決定するには、異なる温度、電圧、湿度レベルで実験計画を立てて、評価試験を実施することが必要です。
MF-capは、Al-Ecapに比べてリプル電流に対する発熱が小さいものの、湿度に対して劣化が進みやすい傾向があります。このため、温度と電圧に加えて湿度を考慮した寿命推定式(式(35))が提案されています*39 。

*39 Huai Wang, et.a al., “Reliability of Capacitors for DC-Link Applications in Power Electronic Converters, An Overview” IEEE Transactions on Industry Application, Vol. 50, NO. 5, 2014
また実際のアプリケーションにより近い条件で評価することも重要です。例えば、ソーラーインバータの稼働では、電圧がゼロで温度20°Cの時間が50%、電圧が最大で温度が90°Cに達する時間が20%、電圧が最大で温度が60°Cの時間が30%です。それぞれの稼働条件を三つのパラメータに変換することで、実用上の期待寿命が求められます。
前述したように、MF-capの寿命推定式は、基礎理論から導き出されたものではなく、実験データに合わせて経験的に導き出されたものであるため、メーカごとに異なります。これはメーカによって、使用している材料の化学的性質、コンデンサのトポロジー、試験方法等が異なる可能性があるためです。あるメーカの寿命推定式を別のメーカの製品に適用する際には注意が必要ですので、ご使用の際にはメーカのカウンセリングをお薦めします。
積層セラミックコンデンサ(MLCC)の寿命推定
MLCCの故障で注目すべきパラメータは静電容量です。MLCCは、(36)式に従って使用中に静電容量が劣化する傾向があります*40。

*40 W. Mason, “Aging of the properties of barium titanate and related ferroelectric ceramics," Journal of the Acoustical Society of America, vol. 27, no. 1, pp. 73-85, 1955. [126]
*41 I. Burn, Ceramics and Glasses, S. Schneider, Ed. ASTM, 1991, vol. 4. [127]
この経年変化は、キュリー温度*42からの冷却に伴うセラミックの強誘電性と体積応答によるものです。MLCCの静電容量は、キュリー温度以上で1~4時間加熱することで回復することも知られています。MLCCメーカは、キュリー温度を下げて加熱によるコンデンサの容量回復を容易にするため、セラミックにドーピング材料を添加する技術があります。
*42 キュリー温度は、強磁性材料が常磁性になる温度です。この点で、熱エネルギーがドメインの磁気モーメント間の引力に打ち勝ち、磁気スピンが材料内でランダムになります。
他のコンデンサと同様にMLCC にも電圧依存の寿命加速があります。この劣化は、アバランシェ破壊*43につながるプール-フレンケル放出*44によるものと考えられています。MLCCの寿命は、電力に昇圧された印加電圧に反比例し、セラミックのタイプや形態に大きく依存します。例えば、剥離、クラック、空隙、細孔などは、平均値よりもはるかに大きな局所電界をもたらす可能性があります。
*43 B. Rawal et. al., “Conduction and failure mechanisms in barium titanate based ceramics under highly accelerated conditions," in Proceedings of the 34th Electronic Components Conference, 1984, pp. 184-188. [99]
*44 E. Loh, “Development of a model for voltage degradation of various dielectric materials," IEEE Transactions on Components, Hybrids, and Manufacturing Technology, vol. 4, pp. 536-544, 1981.[128]
MLCCに電圧加速試験を行ったときに、故障が発生する時間 t と印加電圧 V との関係は式(37)で表されます。厚さ25μmのBaTiO3誘電体に50~150Vを印加した場合の電圧加速係数 N は2.6との報告があります*45。誘電体層が厚い場合は、平均内部電界が減少するため、Nの値は1.2まで低下するとされ*40、一般的には電圧加速係数 N は1~3が使われています。

*45 J. Minford et. al.,” Accelerated aging study of multilayer ceramic capacitors," in American Ceramic Society Annual Meeting, Cincinnati, Ohio, 1979. [129]
この電圧加速寿命は、温度依存の影響を考慮していません。温度上昇下での漏れ電流の増加は、一般に熱暴走によるものです。この熱暴走は、一般にセラミックに内在する要因によって引き起こされます。これらの内在的要因は、セラミック内部の電子障害、転位、粒界などです。
MLCCでは、アバランシェ絶縁破壊と熱絶縁破壊の両方が発生します。2つの絶縁破壊モードの組み合わせた故障発生時間は、式(38)であらわすことができます*46。

*46 T. Prokopowicz and A. Vaskas, “Research and development, intrinsic reliability, subminiature ceramic capacitors," Sprague Electric Corporation, Tech. Rep., Oct. 1969. [130]
*47 ( =*42) B. Rawal et. al.,“Conduction and failure mechanisms in barium titanate based ceramics under highly accelerated conditions," in Proceedings of the 34th Electronic Components Conference, 1984, pp. 184-188. [99]
この式は、JIS や MIL-STD の試験条件(CR>20 MF、定格電圧の200% 、85℃、1000 時間)におけるMLCC のデータによく適合することが示されています*48, 49。
*48 W. Minford, “Accelerated life testing and reliability of high-k multilayer ceramic capacitors," IEEE Transactions on Components, Hybrids, and Manufacturing Technology, vol. 5, no. 3, pp. 297-300, 1982.[131]
*49 ( =*42) R. Munikoti and P. Dhar, “Highly accelerated life testing (halt) for multilayer ceramic capacitor qualification,“ IEEE Transactions on Components, Hybrids, and Manufacturing Technology, vol. 11, no. 4, pp. 342-345, 1988. [132]
まとめ(一般的な寿命推定のパラメータ)
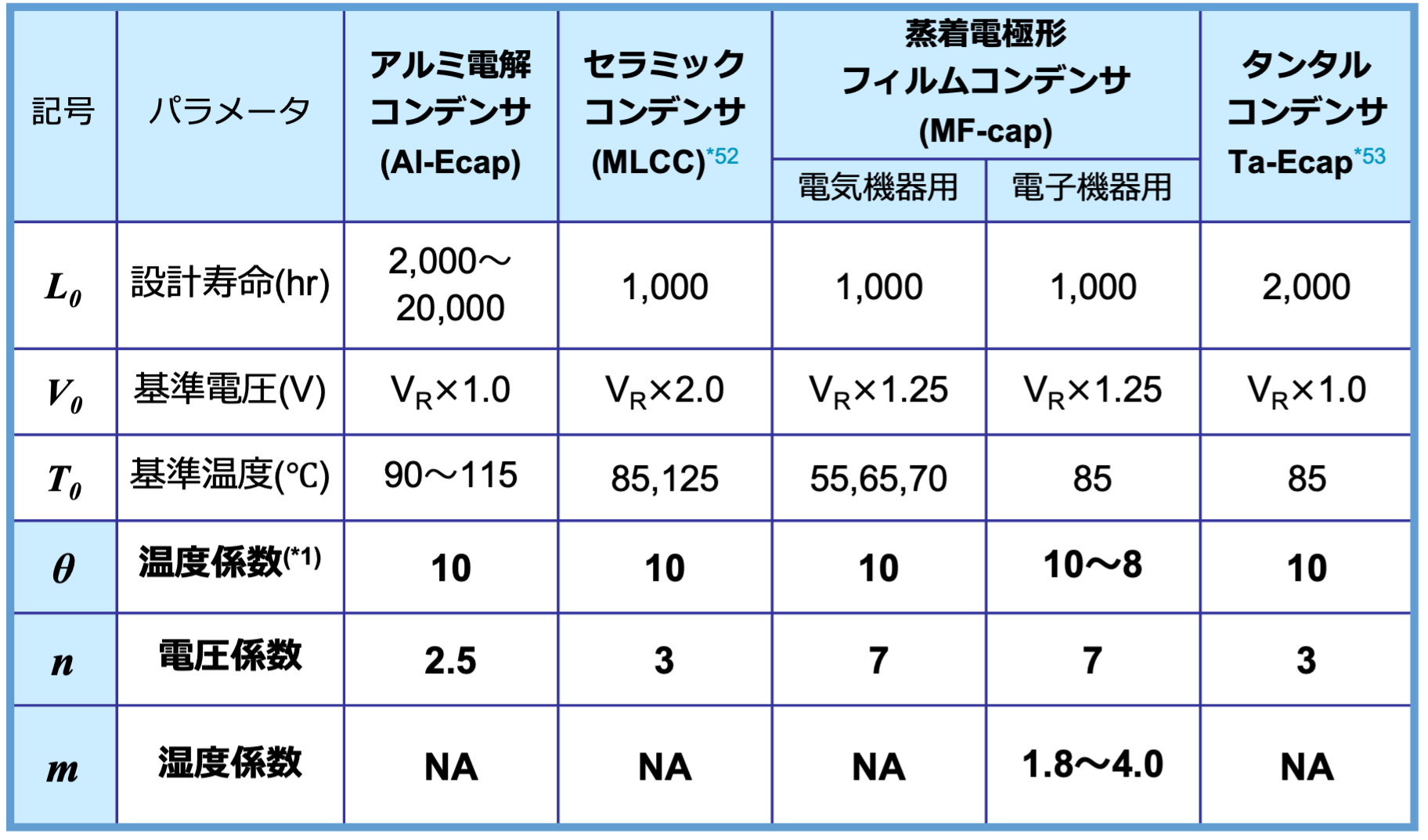
コンデンサの寿命推定は、主に温度加速と電圧加速を考慮した実験式が用いられます。またMF-capでは、湿度もストレス要因に加える必要があります。ただしそれらの加速係数はコンデンサの種類によって異なります。このため、温度係数 θ、電圧加速係数 n、湿度加速係数 m は、コンデンサ毎に、異なる温度、電圧、湿度レベルでの評価試験を行い、各係数に関する活性化エネルギー Ea を求めることで決定できます。
表1に各コンデンサの寿命推定のパラメータと係数をまとめました。
温度加速は、一般的に10℃2倍則が使われていますが、50~60℃といった実用温度付近や最高使用温度を越えた温度では適合性が異なる場合があります。またはMF-capでは、定格温度を8℃超えるごとに寿命が半分になるとする「8℃2倍則」を提案する場合があるため、メーカへ確認が必要です
当社ではAl-capの電圧加速係数を2.5としていますが、メーカや種類(固体電解質形、電解液形等)によって、2~5の値を採用しています。
同様に当社のMF-capの電圧加速係数を7としていますが、誘電体の種類や厚さによって10~20の値が使われる場合があります。また湿度による影響(電圧加速 KRH-MFC)でご説明したMF-capの湿度加速係数には、一般的に使われる値はありませんが、1.8~4の値が多く報告されています*50, 51。
*50 https://www.reaj.jp/pdf/event/2021/0531-1-1.pdf
*51 Huai Wang., “Capacitor Failure Modes and Lifetime Models from an Application Perspective”, PSMA and PELS Capacitor Workshop 2018
*52 Jung-Rag Yoon and Kyung-Min Lee, “Analysis the Reliability of Multilayer Ceramic Capacitor with inner Ni Electrode under highly Accelerated Life Test Conditions”, TRANSACTIONS ON ELECTRICAL AND ELECTRONIC MATERIALS VOL. 10, NO. 1, FEBRUARY 25, 2009
*53 https://nepp.nasa.gov/files/24717/Teverovsky_2013_n258_VoltageAcceleration_CPMT_pres.pdf

監修/飯田 和幸
エーアイシーテック株式会社 ゼネラルアドバイザー
1956年埼玉県生まれ。
日立化成株式会社、日立エーアイシー株式会社にてコンデンサの製品開発と高機能化、コンデンサ用の金属材料や有機材料開発、マーケティング業務に従事。
広報誌、業界誌、各種便覧等にコンデンサに関する記事を寄稿。
2005年から2015年まで株式会社 日立製作所 技術研修所でコンデンサの使い方に関する講座を担当。
2020年よりエーアイシーテック株式会社 ゼネラルアドバイザー。
- 「タンタル電解キャパシタ」
電気化学会編 丸善 電気化学便覧 第5版 15章 キャパシタ 15.2.4節 b (1998) - 「タンタル・ニオブコンデンサの開発動向と材料技術」
技術情報協会セミナー 2008年6月 - 「鉛フリー対応表面実装形フィルムコンデンサ MMX-EC, MML-ECシリーズ」
日立化成テクニカルレポート 48号 製品紹介 2007年 - 「電子機器用フィルムキャパシタ」
丸善 キャパシタ便覧 第5版 5章 フィルムキャパシタ 5.2項 (2009) - 「新エネルギー用大型フィルムコンデンサMLCシリーズ」
新神戸電機株式会社 新神戸テクニカルレポート 22号(2012)
